

Source of Water Supply
Sources of water supply
In nature water occurs abundantly as:
- water vapour in the atmosphere,
- as liquid water in inland waters and the ocean,
- as ice in polar regions, and
- as water of hydration in many rocks and minerals in the earth’s crust.
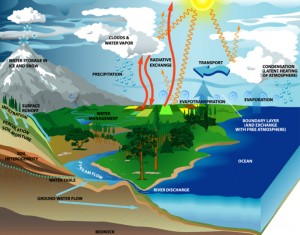
Water Supply Sources
The original source of all natural water supplies is, however, rain. Rain water, in its passage Through the air, dissolves many of the soluble gases present in the atmosphere and in percolating through the various strata of the earth, collects mineral salts and other impurities. These may be either acidic or alkaline. Of the dissolved gases, oxygen and carbon dioxide are the most important. The dissolved minerals include bicarbonates, carbonates, chlorides, sulphates and nitrates of calcium, magnesium, sodium and sometimes iron also. Silica may also be Po and in places. The water available may also contain suspended matters—both mineral and organic.
- The quality of water depends entirely upon its source of supply.
Rain Water: Rain water is the purest form of water but to be absolutely pure it should be collected after a heavy shower, because prior to that, the water may contain dissolved gases and also dust. In industrial areas, gases in the atmosphere contaminate rain water, e.g., sulphuric acid. Dissolved carbon dioxide renders water acidic and increases its solvent power. When this acidic water passes through the soil, it reacts with the calcium and magnesium carbonates present in the soil and forms bicarbonates. Pure rain water is soft.
River Water: River and canal waters are inland waters fed by rains. These are less pure than rain water as they contain dissolved chemicals. Their composition is subject to considerable variation depending on the areas over which they are towing and the soluble chemical salts present in the roci:s and soil. Dissolved solids in the river water also vary with the rate of flow. The impurities in river water are generally the chlorides, sulphates, carbonates and bicarbonates of calcium, magnesium and iron. The soluble bicarbonates of calcium and magnesium are formed by the action of dissolved carbon dioxide upon insoluble carbonates. The presence of soluble calcium and magnesium salts in river water makes it hard. Besides this, river and canal waters are liable to be contaminated with sewage and sludges of cities by which they flow and also organic matter, ammonia and nitrites.
Spring and Well Water: This is percolated rain water whicn, on reaching the ground, passes through the various strata of the soil, thereby dissolving the soluble salts of the soil. This water is extremely clear as a result of natural filtration through sand beds and strata. The chief difference between spring and well water and river water is that the former contains a much higher percentage of dissolved mineral matter although it is free from organic impurities and ammonia, and often has a palatable taste and in most cases, may be used for drinking. Water from springs and wells is extremely hard.
Sea Water: Rivers carry a large volume of water with dissolved impurities into the sea and, as such, the sea contains the maximum amount of dissolved impurities. The total dissolved impurities in sea water are about 3.6 per cent of which 2.6 per cent is common salt; others are magnesium chloride, magnesium sulphate, calcium sulphate, potassium chloride, magnesium bromide and traces of iodides, silica, etc. The quantity of dissolved salts is very much greater in inland seas. Sea water is saline, hence unsuitable for drinking purposes and is hard. Sea water is also faintly alkaline.
Surface Water and Ground Water: As rain falls on the earth, it flows into streams as surface runoff, passes into the air as vapour and goes down into the ground. It is then recovered as surface water or ground water.
The term surface water indicates natural water in rivers, streams, ponds and lakes, although a part of such deposits of water may have percolated more or less through the soil in the course of its flow along the earth’s surface. As a result, the water absorbs a part of the materials with which it comes in contact. Surface water, therefore, indicates the chemical constitution and physical conditions of the area in question.
The water obtained from springs and wells in a given locality may be very different from the local surface water. Ground water also indicates the local geological strata and contains a greater percentage of dissolved salts. Ground water is inore nearly constant in composition. Some of the ground water may be hot and may contain dissolved gases. It is sometimes used for medicinal baths. Ground water may be different in taste and chemical character—acid, alkaline, bitter, hepatic, ferruginous, iodinous or siliceous.
__________________________________________________________
All About Water
A comprehensive, interesting source of information about water treatment alternatives, bottled water quality, and water filter products, including a listing of several general water facts.
2 Responses to “Source of Water Supply”
Leave a Reply






 LIKE TO GET UPDATES
LIKE TO GET UPDATES  TO GET EXPERT GUIDE
TO GET EXPERT GUIDE
IT IS A VERY GOOD SITE. WE GET EVERYTHING HERE THAT’S ALL I HAD TO SAY
whoah this blog is wonderful i love studying your posts. Keep up the good paintings! You already know, a lot of persons are looking round for this info, you can aid them greatly.